13.1.2圆柱、圆锥、圆台和球教学设计-苏教版高中数学必修第二册

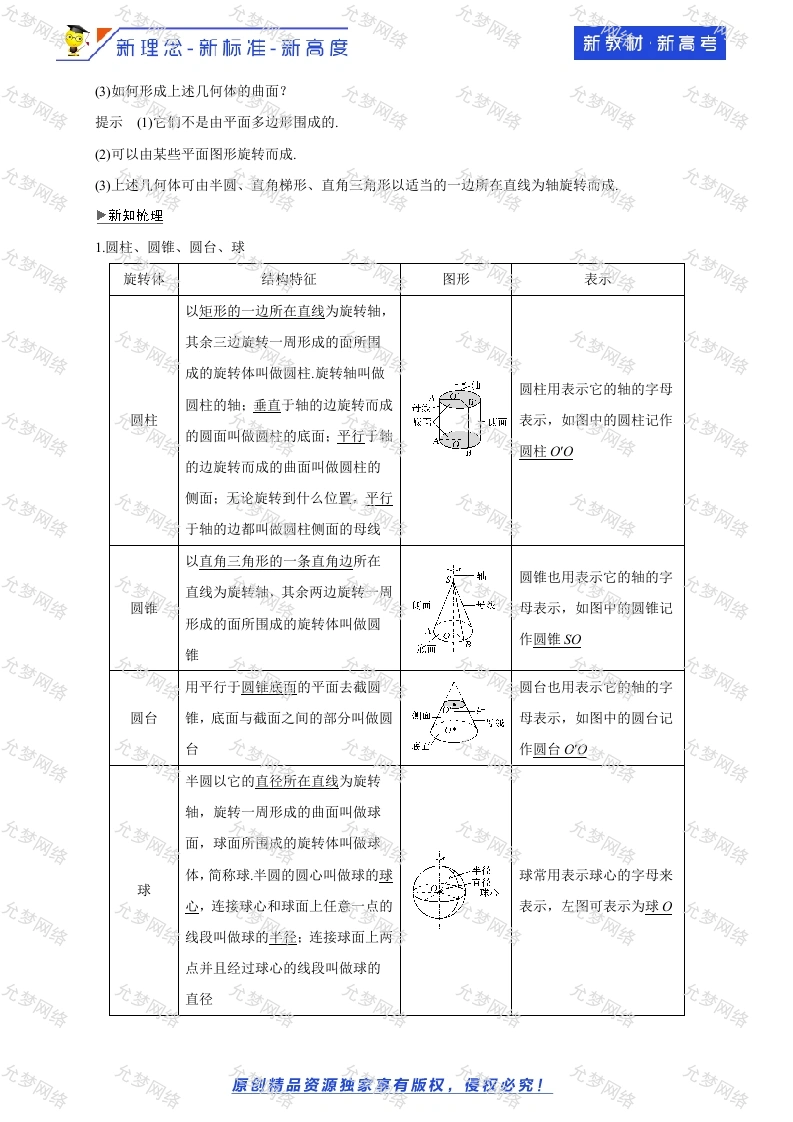
新理念-新标准-新高度新教材·新高考第十三章立体几何初步13.1.2圆柱、圆锥、圆台和球教材分析立体几何是研究三维空间中物体的形状、大小和位置关系的一门数学学科，而三维空间是人们生存发展的现实空间.所以，学习立体几何对我们认识、理解现实世界，更好地生存与发展具有重要的意义.《立体几何初步》一章，是在义务教育阶段“空间与图形”课程的延续与发展，教材的编写力图凸显《普通高中数学课程标准》（以下简称《课程标准》）对立体几何的教学要求，通过直观感知、操作确认、思辩论证、度量计算等方法，以帮助学生实现逐步形成空间想像能力这一教学目的。教学目标与核心素养课程目标学科素养1认识圆柱、圆锥、圆台的结构特征，在旋转体与简单组合体概念的形成中，经历由具2.认识柱、锥、台、球及其复杂的空间图形体到抽象，由一般到特殊的过程，发展学生的数学抽的结构特征，并能运用这些特征描述现实生象素养和直观想象素养。活中简单物体的结构。教学重难点1教学重点：认识圆柱、圆锥、圆台的结构特征2.教学难点：能运用这些特征描述现实生活中简单物体的结构，课前准备多媒体调试、讲义分发。教学过程惰克引入如图，观察下列实物图.。问题()上述三个实物图抽象出的几何体与多面体有何不同？(②)上述实物图抽象出的几何体中的曲面能否由某些平面图形旋转而成？原创精品资源独家享有版权，侵权必究！新理念-新标准-新高度新教材·新高考3)如何形成上述几何体的曲面？提示()它们不是由平面多边形围成的.(2)可以由某些平面图形旋转而成。(③)上述几何体可由半圆、直角梯形、直角三角形以适当的一边所在直线为轴旋转而成.◆新知枕埋1圆柱、圆锥、圆台、球旋转体结构特征图形表示以矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱用表示它的轴的字母圆柱的轴：垂直于轴的边旋转而成计流圆柱表示，如图中的圆柱记作的圆面叫做圆柱的底面：平行于轴圆柱O'O的边旋转而成的曲面叫做圆柱的侧面：无论旋转到什么位置，平行于轴的边都叫做圆柱侧面的母线以直角三角形的一条直角边所在圆锥也用表示它的轴的字直线为旋转轴，其余两边旋转一周圆锥Lmi母表示，如图中的圆锥记形成的面所围成的旋转体叫做圆作圆锥SO锥而用平行于圆锥底面的平面去截圆圆台也用表示它的轴的字圆台锥，底面与截面之间的部分叫做圆母表示，如图中的圆台记台作圆台O'0半圆以它的直径所在直线为旋转轴，旋转一周形成的曲面叫做球面，球面所围成的旋转体叫做球体，简称球半圆的圆心叫做球的球球常用表示球心的字母来球心，连接球心和球面上任意一点的表示，左图可表示为球O线段叫做球的半径：连接球面上两点并且经过球心的线段叫做球的直径原创精品资源独家享有版权，侵权必究！新理念-新标准-新高度新教材·新高考题型一旋转体的结构特征【例1】给出下列命题：①圆柱的母线与它的轴可以不平行：②圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形：③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线：④圆柱的任意两条母线所在的直线是互相平行的其中正确的是(A.①②B.②③c.①③D.②④解析由圆柱、圆锥、圆台的定义及母线的性质可知②④正确，①③错误.答案D规律方法由简单旋转体判断问题的解题策略()准确掌握圆柱、圆锥、圆台和球的生成过程及其特征性质是解决此类概念问题的关键，(②)解题时要注意两个明确：①明确由哪个平面图形旋转而成：②明确旋转轴是哪条直线，【训练1】下列命题正确的是(只填序号)①以直角三角形的一边所在直线为轴旋转一周所得的旋转体是圆锥：②以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台：③圆柱、圆锥、圆台的底面都是圆：④以等腰三角形的底边上的高所在直线为旋转轴，其余各边旋转180°形成的曲面围成的几何体是圆锥：⑤球面上四个不同的点一定不在同一平面内：⑥球的半径是球面上任意一点和球心的连线段，解析①以直角三角形的一条直角边所在直线为轴旋转一周才可以得到圆锥：②以直角梯形垂直于底边的一腰所在直线为轴旋转一周才可以得到圆台：③它们的底面为圆面：④正确：作球的一个截面，在截面的圆周上任意取四个不同的点，则这四点就在球面上，故⑤错误：根据球的半径定义，知⑥正确，答案④⑥题型二简单组合体的结构特征【例2】指出图中三个几何体的构成，原创精品资源独家享有版权，侵权必究！